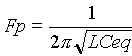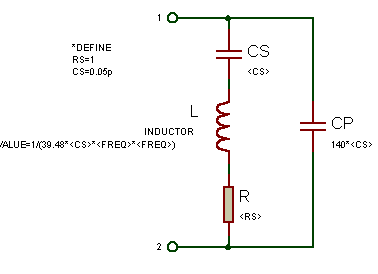
On définit les réactances suivantes :
XL = L.w
XCs = 1/Cs.w
XCp = 1/Cp.w
avec w = 2 pi F
Calcul de la Résonnance parallèle
|
On définit les réactances suivantes : XL = L.w XCs = 1/Cs.w XCp = 1/Cp.w avec w = 2 pi F |
Pour F=Fs résonnance série XL = XCs. On déduit :
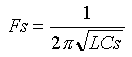
Pour F > Fs l'impédance série devient inductive car XL augmente et XCs diminue (w= 2 pi F augmente). La réactance série vaut alors XL-XCs
Elle peut alors résonner avec Cp (résonnance //) et en F=Fp on
a XL-Xcs=XCp =>XL=XCs+XCp => Lw=(1/Cp.w+1/Cs.w).
Si on pos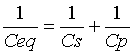e : 
Ceq (équivalent ) est l'ensemble Cs et Cp en série donc très
peu inférieur à Cs (le plus petit des deux) car Cp=140Cs. On obtient
alors Lw=1/Ceqw =>
w*w=1/LCeq soit encore